Sincere thanks to my kind classmate Xinghao Jiang for lending me the fluid mechanics textbook, which helped me review the fundamentals of fluid mechanics.

Introduction of Navier-Stokes Equations

The Navier-Stokes equations, abbreviated as NS, is an equation based on Newton’s second law that describes the motion of a given particle in a fluid using Euler notation. By solving this equation, we would be able to obtain the velocity field of the fluid and thus understand its motion, making it valuable in fields such as precision instrument manufacturing and oceanographic research.

We are all very familiar with Newton’s second law, which states that the net force acting on an object is equal to the product of its mass and acceleration, i.e. \(\boldsymbol{F}=m\boldsymbol{a}\). The bold symbol denotes a vector, meaning this variable has both magnitude and direction. If you replace the acceleration as the derivative of velocity \(\boldsymbol{V}\) with respect to time \(t\) yields a partial differential equation in terms of velocity. For an individual particle moving in infinite space, integrating both sides of the equation with respect to time gives us the particle’s motion equation. However, for a system of particles like a fluid, this method is no longer applicable due to the presence of the velocity field. That is when we introduce the Euler Notation and material derivative.

\[m\frac{d\boldsymbol{V}}{dt}=\boldsymbol{F}\rightrightarrows \boldsymbol{V}=\frac{\int{F}dt}{m} + \boldsymbol{V}_{0}\]

Euler Notation

Unlike a single particle, fluid can be considered as a set of continous particles. Therefore, we need to construct a function that describes the distribution of the motion state over the entire fluid space, which is stated as a field function. The most intuitive method is to assume that the velocity field function at a given point in space and time to be \(\boldsymbol{V}=\boldsymbol{V}(x,y,z,t)\). It should be noticed that here \((x,y,z)\) denotes a given position in space instead of the location of a given particle. In this way, if x, y, and z are given, the velocity field function represents the velocity of the fluid element that flows to that position at different times. This is so called Euler Notation. Other than velocity, any other kinds of physical variables can be expression following Eluer notation, such as temperature \(T\), position \(\boldsymbol{r}\), salinity\(S\), and so on. In addition, there is also the Lagrangian Notation, but we won’t discuss it in detail here.

Material Derivative

However, the Euler notation introduces a new problem: how to represent the motion state of a given particle using Euler notation in fluid? Don’t panic, we can simply assume that there is a given particle in the fluid, and during time \(\delta t\), it moves from point A to point B with a certain velocity. The spatial and temporal location of A and B are respectively \((x,y,z,t), (x+\delta x, y+\delta y, z+\delta z, t+\delta t)\). We can use the Euler notation to describe its acceleration during this process.

\[\boldsymbol{a}=\frac{\boldsymbol{V}(x+\delta x, y+\delta y, z+\delta z, t+\delta t)-\boldsymbol{V}(x,y,z,t)}{\delta t}\]

Let the velocity be continously differentiable. This allows us to expand \(\boldsymbol{V}(x+\delta x, y+\delta y, z+\delta z, t+\delta t)\) to the first order.

\[\boldsymbol{V}(x+\delta x, y+\delta y, z+\delta z, t+\delta t) = \boldsymbol{V}(x,y,z,t) + \frac{\partial \boldsymbol{V}}{\partial x}\delta x + \frac{\partial \boldsymbol{V}}{\partial y}\delta y + \frac{\partial \boldsymbol{V}}{\partial z}\delta z + \frac{\partial \boldsymbol{V}}{\partial t}\delta t\]

Now, substituting the above expressiono into the acceleration equation, and supposing we have a very very small duration of time, i.e. let \(\delta t \rightarrow 0\), then we would have

\[\lim_{\delta t\to 0} \boldsymbol{a} = \frac{\partial \boldsymbol{V}}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial \boldsymbol{V}}{\partial y}\frac{\partial y}{\partial t} + \frac{\partial \boldsymbol{V}}{\partial z}\frac{\partial z}{\partial t} + \frac{\partial \boldsymbol{V}}{\partial t}\]

To simplify the above expression, let \(u, v, w\) be the velocity projection along \(x, y, z\) axes. And the capital letter \(D=\partial/\partial t+(\boldsymbol{V}\cdot\nabla)\), in this way, we can orgnize the above equation into a more simplified form.

\[\lim_{\delta t\to 0} \boldsymbol{a} = \frac{D\boldsymbol{V}}{Dt}\]

Not only can the velocity of a particle be expressed in this way, but the change rate of all physical quantities for a given particle in a fluid can be written in this form. For example, the temperature variation rate of a given particle in the fluid is

\[\frac{DT}{Dt}=\frac{\partial T}{\partial t}+(\boldsymbol{V}\cdot\nabla)T\]

Now, this representation of the change rate of physical quantities for a particle in a fluid with respect to time is called the material derivative.

Newton’s Second Law to NS Equations

With the help of material derivative, we are able to describe the second Newton’s law in the fluid.

\[\begin{aligned} \rho\frac{D\boldsymbol{V}}{Dt}=\boldsymbol{f}\\ \frac{\partial \boldsymbol{V}}{\partial t}+(\boldsymbol{V}\cdot\nabla)\boldsymbol{V}=\frac{\boldsymbol{f}}{\rho} \end{aligned}\]

Note that here \(\rho\) stands for the density of fluid, normally we assume the fluid to be incompressible so that \(\rho\) becomes constant. If the fluid is comressible, then there would be a density field as well, which would make the expression become much more complicated. Now, with incompressible fluid assumption, once the force density is substituted into the equation, the motion of the fluid under the specific force can be obtained.

This leads us to a new question. How many kinds of forces are there? Gravity for sure. But what about pressure stress and viscous stress. Here let us solve it one by one.

Pressure Stress

Apart from gravity, water particles are also subjected to pressure in the opposite direction of the normal to the force surface. To visualize this process, we normally assume a cubic element in the fluid space. See figure below.

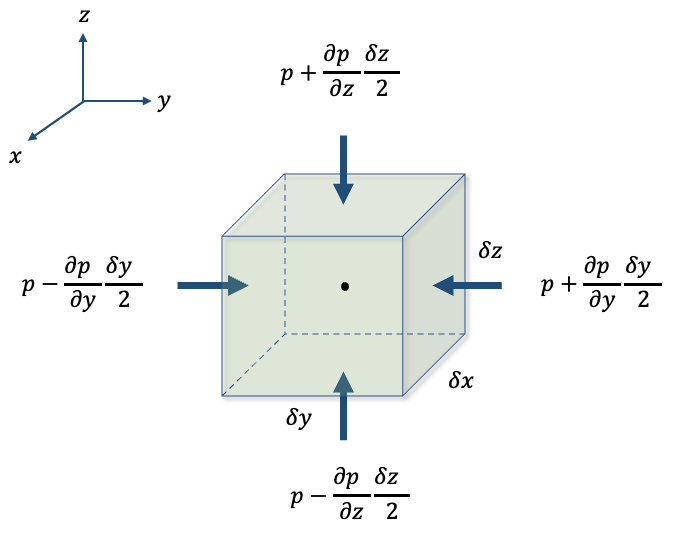
Surface pressure of the cubic fluid element

\(p\) denotes the pressure at the center position of the cubic fluid element. Since the size of the cubic element is extremely small, we can replace the pressure difference \(\Delta p_{x}\) between center position and the cubic surface with the product of first-time derivative and the their distance \(\frac{\partial p}{\partial x}\frac{\delta x}{2}\). That gives us the expressions in the above figure.

Now, pressure stress can be easily calculated by multiplying pressure with the area of surfaces.

  • Pressure stress along along positive direction of x axis.
\[(p-\frac{\partial p}{\partial x}\frac{\delta x}{2})\delta y\delta z - (p+\frac{\partial p}{\partial x}\frac{\delta x}{2})\delta y\delta z = -\frac{\partial p}{\partial x}\delta x\delta y\delta z\]
  • Pressure stress along along positive direction of y axis.
\[(p-\frac{\partial p}{\partial y}\frac{\delta y}{2})\delta x\delta z - (p+\frac{\partial p}{\partial y}\frac{\delta y}{2})\delta x\delta z = -\frac{\partial p}{\partial y}\delta x\delta y\delta z\]
  • Pressure stress along along positive direction of z axis.
\[(p-\frac{\partial p}{\partial z}\frac{\delta z}{2})\delta x\delta y - (p+\frac{\partial p}{\partial z}\frac{\delta z}{2})\delta x\delta y = -\frac{\partial p}{\partial z}\delta x\delta y\delta z\]

The total pressure stress the cubic fluid element subjected to is

\[-\nabla p\times\delta x\delta y\delta z\]

Thus, the pressure stress density is \(-\nabla p\).

Viscous Stress

Unlike pressure stress, viscous stress differs in magnitude and amplitude at different positions. For example, for a given surface perpendicular to x axis, the viscous stress varies quite rapidly, making it rather difficult to describe it by simply a normal vector.

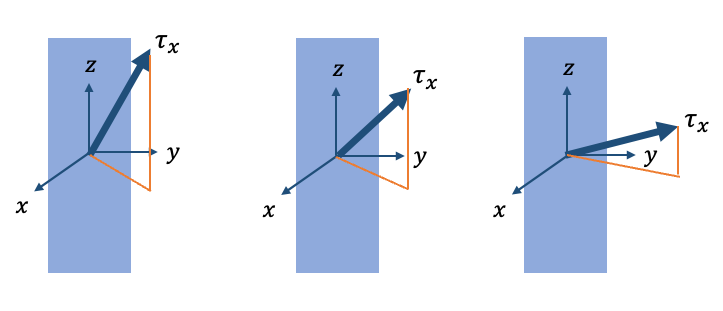
\(\tau_{x}\) denotes the viscous stress whom the plane is subjected to.

How can we desribe this complicated forces now? Well, we just need to further decompose the viscous stress into 3 dimensions, for example we let \(\boldsymbol{\tau_x}=\tau_{xx}\boldsymbol{i}+\tau_{xy}\boldsymbol{j}+\tau_{xz}\boldsymbol{k}\). Similarly, the viscous stress at y-perpendicular and z-perpendicular plane can be decomposed as \(\boldsymbol{\tau_y}=\tau_{yx}\boldsymbol{i}+\tau_{yy}\boldsymbol{j}+\tau_{yz}\boldsymbol{k}\) and \(\boldsymbol{\tau_z}=\tau_{zx}\boldsymbol{i}+\tau_{zy}\boldsymbol{j}+\tau_{zz}\boldsymbol{k}\). Remember that the first subscript means which plane the viscous stress is applied to, and the second subscript means the direction of the viscous stress. With the help of further decomposed analysis, we reorgnize the viscous stress to 3 axis by adding the same direction viscous projection, i.e.

\[\begin{aligned} \tau_{sx}=\tau_{xx}+\tau_{yx}+\tau_{zx}\\ \tau_{sy}=\tau_{xy}+\tau_{yy}+\tau_{zy}\\ \tau_{sz}=\tau_{xz}+\tau_{yz}+\tau_{zz} \end{aligned}\]

The subscript \(sx\) means this physical parameter is parallel to the positive direction of x axis.