Coriolis Force
Derivation of Coriolis Force
Supposing that we have 2 coordinates whoes origins both locate at the center of the Earth. The red one is absolutely static and the green one rotates along with our planet. See below.
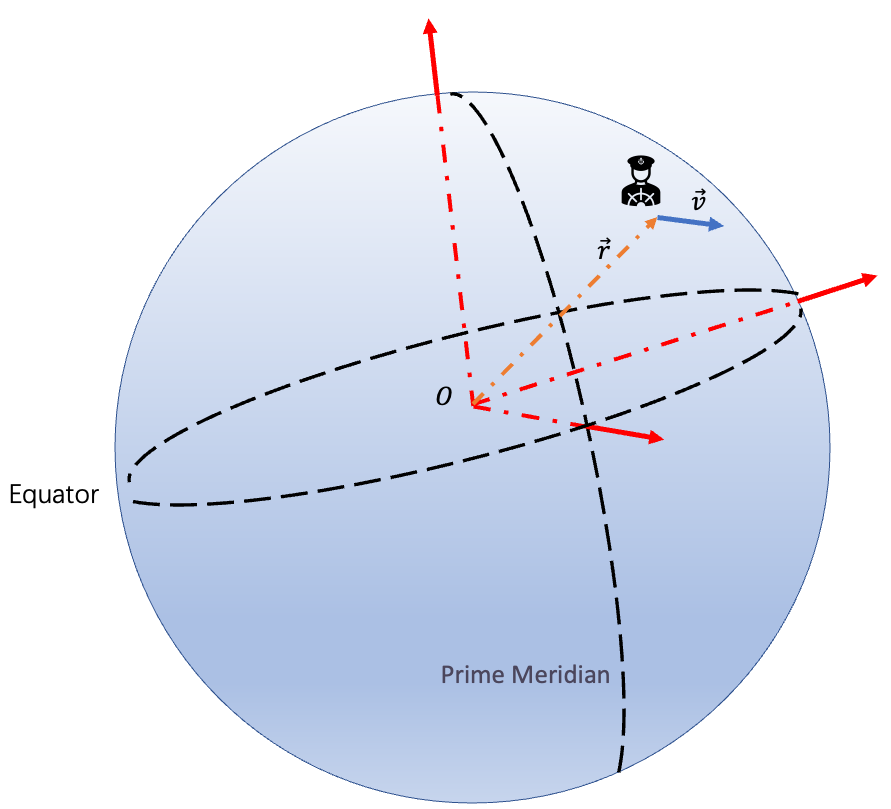
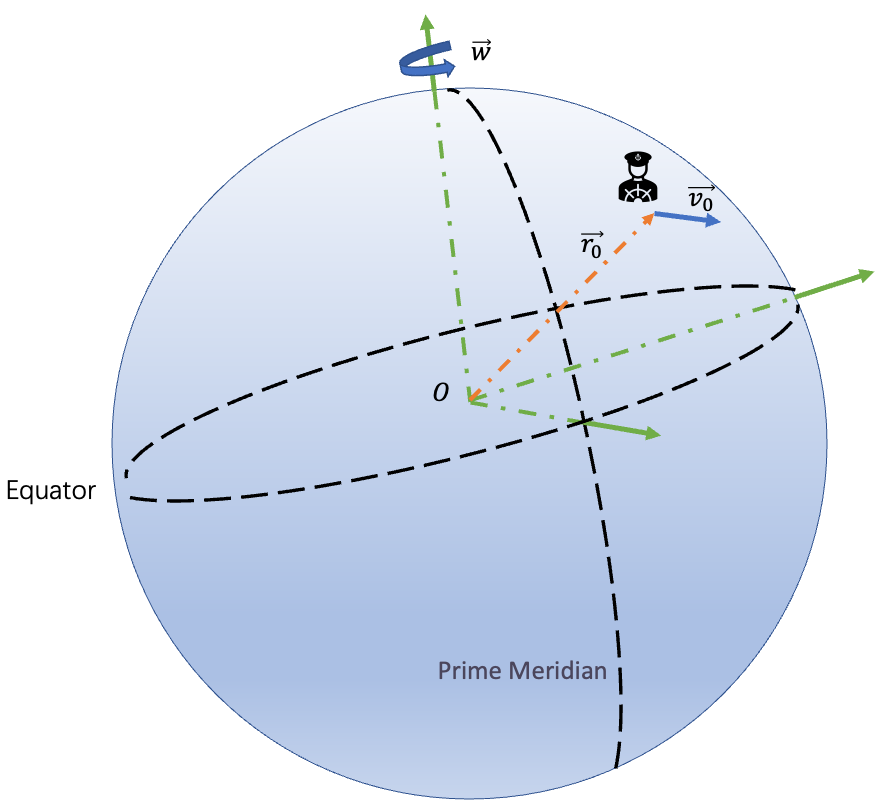
Now, assuming that there is a car running on the street at \(\overrightarrow{v_0}\) to the policeman’s eyes. Well, if we view this scene from the space view, the velocity in our eyes should be the sum of the rotation speed of the earth and the car running along the street. That gives us:
\[\overrightarrow{v}=\overrightarrow{v_0}+\overrightarrow{\omega}\times\overrightarrow{r_0}\]Therefore the acceleration with respect to the static coordinate is
\[\begin{aligned} \overrightarrow{a}&=\frac{d\overrightarrow{v}}{dt} + \overrightarrow{\omega}\times\overrightarrow{v}\\ &=\frac{d\overrightarrow{v_0}}{dt}+\overrightarrow{\omega}\times\frac{d\overrightarrow{r_0}}{dt}+\overrightarrow{\omega}\times\overrightarrow{v_0} +\overrightarrow{\omega}\times\overrightarrow{\omega}\times\overrightarrow{r_0}\\ &=\frac{d^2\overrightarrow{r_0}}{dt^2}+2\overrightarrow{\omega}\times\frac{d\overrightarrow{r_0}}{dt} +\overrightarrow{\omega}\times\overrightarrow{\omega}\times\overrightarrow{r_0} \end{aligned}\]Following the traditions in Physics, the second and third term is usually set to be negative. In this way, Earth’s surface objects experience a net external force of
\[\overrightarrow{F'}=\overrightarrow{F}-(-2m\overrightarrow{\omega}\times\frac{d\overrightarrow{r_0}}{dt})-(-m\overrightarrow{\omega}\times\overrightarrow{\omega}\times\overrightarrow{r_0})\]Where the second term is so called Coriolis Force, i.e. \(\overrightarrow{C}=-2m\overrightarrow{\omega}\times\frac{d\overrightarrow{r_0}}{dt}\).
Though we see this Coriolis term in the net force of an object, there isn’t real such a force exerted by some other objects to the one we focus on. More likely, this term origins the mathematical consistency while mapping physical vectors from a rotating coordinate to the inertial coordinate.
Coriolis-induced Turning Effect
There are already conlusions about the motion distortion effect induced by the Coriolis force. Such as, the objects in the North hemisphere experiences a Coriolis force to the right in the direction of motion, while objects from the South hemisphere are subjected to a left side Coriolis force. Why is that? Now let’s try to explain it with some basic calculations.
First, we switch to a surface coordinate on our planet. The y axis goes along the longitude to north pole and the x axis goes along the latitude from West to East, making our z axis rises towards the sky. Refer to the following figure.
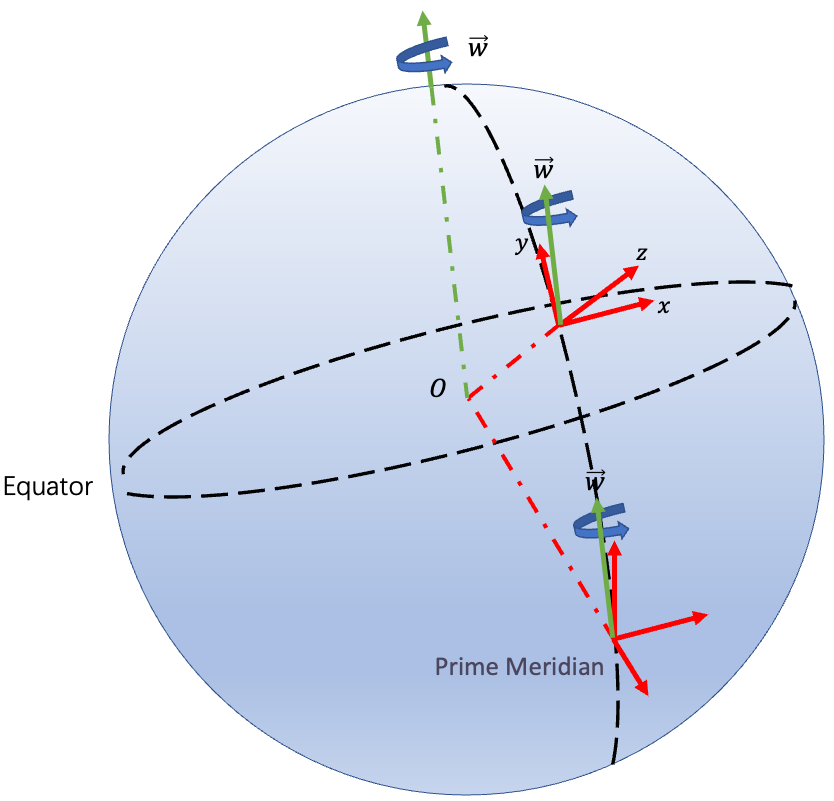
We let the angular velocity in the given coordinate be like \(\overrightarrow{\omega}=\omega_y\overrightarrow{j}+\omega_z\overrightarrow{k}\). Since the angular velocity is perpendicular to the equator plane, \(\overrightarrow{\omega_x}\) must equal to 0. And if we were at the North hemisphere, the angular z component must be no smaller than 0 while in the South hemisphere, z component remain smaller than or equal 0. Check out the table for details.

Now, imagine that the object only moves along the xoy plane, that gives us \(\overrightarrow{v_0}=v_x\overrightarrow{i}+v_y\overrightarrow{j}\). Simply substitude the object velocity and angular velocity into the Coriolis force expression, we get
\[\begin{aligned} \overrightarrow{C}&=-2m(\omega_y\overrightarrow{j}+\omega_z\overrightarrow{k})\times(v_x\overrightarrow{i}+v_y\overrightarrow{j})\\ &=2m(\omega_z v_y\overrightarrow{i}-\omega_z v_x\overrightarrow{j} +\omega_y v_x\overrightarrow{k}) \end{aligned}\]Here, we ignore the force component along the z axis. See what if we dot times the rest force and the object velocity. You can easily see that
\[\overrightarrow{C}_{xoy}\cdot \overrightarrow{v_0}=2m(\omega_z v_y v_x-\omega_z v_x v_y)=0\]Shockingly, we see the horizontal component of the coriolis force always is perpendicular to the object velocity, and if we go further, let’s assume that \(v_y=0\), we would have that \(\overrightarrow{C}=-2m\omega_z v_x\overrightarrow{j}\) and \(\overrightarrow{v_0}=v_x\overrightarrow{i}\). Apart from the always identical parameter \(v_x\) and always positive parameter \(2m\), we can see that the location of coriolis force is determined by z-component angular velocity.
Wow! Then according to the above table, in the North hemisphere, the coriolis force are always locate at the right side of the object velocity, and the contrary at South hemisphere. In conclusion, we have
1. Coriolis force is perpendicular to the object velocity.
2. In the North hemisphere, C at V's right side.
3. In the South hemisphere, C at V's left side.